EXKLUZIVNĚ: Šoky a zklamání: Jak překvapivé bylo mistrovství světa 2022?
29.05.2023 20:15
Přinášíme vám exkluzivní překlad odborného článku od sázkového analytika Josepha Buchdahla, který spravuje webové stránky www.football-data.co.uk, na kterém poskytuje historické výsledky, zápasové statistiky a údaje o kurzech. Je také autorem knih Fixed Odds Sports Betting: Statistical Forecasting & Risk Management (2003), How to Find a Black Cat in a Coal Cellar: The Truth about Sports Tipsters (2013) a Squares & Sharps, Suckers & Sharks: The Science, Psychology & Philosophy of Gambling (2016).
- Jak překvapivé bylo mistrovství světa 2022?
- Pravděpodobnost metodou Monte Carlo
- Outsideři na mistrovství světa
- Šoky a zklamání: část první
Jak šokující bylo mistrovství světa 2022? Bylo vítězství Japonska nad Německem takovým překvapením? Joseph Buchdahl rozebírá data, aby zjistil, zda jsou velká překvapení na tak masivním turnaji opravdu tak překvapivá, jak si myslíme.
Podle společnosti Gracenote, která se zabývá sběrem sportovních metadat, bylo mistrovství světa 2022 v Kataru turnajem outsiderů – 15 zápasů totiž skončilo překvapením (dle jejich vlastní definice) – což je nejvyšší procento za posledních 64 let.
Katar byl nejpřekvapivějším mistrovstvím světa za 64 let.
Jak překvapivé takové číslo ale opravdu je a jak vlastně rozhodnout, že jde o překvapení? Všichni bychom pravděpodobně souhlasili, že vítězství Japonska nad Španělskem a Německem a porážka Argentiny v zápase se Saúdskou Arábií, byly překvapivé. Tato premisa však závisí na tom, nakolik je platné naše přesvědčení, že Španělsko, Německo a Argentina měly tyto zápasy vyhrát. Naše intuice nám možná říká, že zcela jistě měly, pokud však není možné dokonale posoudit skutečnou pravděpodobnost výsledků, měli bychom si vždy uvědomovat možnost potenciální chyby.
Když se zdá být fotbalový výsledek překvapivý, znamená to, že měl outsider – právoplatně považován za outsidera na základě přesného predikčního modelu – jen štěstí nebo je to tím, že ve skutečnosti nebyl outsiderem a predikční model se zmýlil?
Z filozofického hlediska se jedná o zajímavou hádanku, kterou lze jen těžko rozluštit. Zde se setkáváme se dvěma druhy nejistot. Nejistota nebo chyba v platnosti předpovědního modelu se nazývá epistemická nejistota a teoreticky ji lze redukovat lepším modelováním.
Dalším druhem nejistoty je nejistota vnitřní, která je známá jako aleatorní nejistota, obecně známá spíše jako náhoda, štěstí nebo nahodilost. Tuto nejistotu nelze zmenšit. Oddělit epistemickou a aleatorní nejistotu může být zrádné. V tomto páru článků pro Pinnacle se pokusím přispět svou troškou do mlýna. V prvním článku se pokusím prozkoumat faktor překvapení mistrovství světa jako celku.
V druhém článku se dozvíte více o tom, co nám tato zjištění mohou říci o přesnosti (nebo efektivitě) sázkových kurzů sázkových kanceláří a o platnosti jejich předpovědního modelu, pomocí kterého je sestavují.
Pravděpodobnostní kombinace výsledků všech 64 zápasů MS
Pokud odhadneme pravděpodobnosti každého ze tří možných výsledků jednotlivých zápasů na MS ve fotbale, můžeme vytvořit pravděpodobnost každé z 64 možných kombinací výsledků. Jaké pravděpodobnosti výsledků bychom ale měli použít?
Většina ambiciózních sázkařů má nepochybně své vlastní metody výpočtu, ale abych ušetřil čas (a s vědomím, že se jedná o jedny z nejlepších dostupných pravděpodobností), použiji ty, které jsou implikovány závěrečnými kurzy společnosti Pinnacle.
Již několikrát jsem podrobně rozebíral, proč jsou závěrečné kurzy Pinnaclu jedny z nejlepších pro odhadování skutečné pravděpodobnosti jednotlivých výsledků. Pinnacle samozřejmě k těmto kurzům přidává marži, proto o ni kurzy musím nejdříve očistit. Pro tyto účely mám vlastní kalkulačku.
Poté se můžeme pomocí těchto vícenásobných pravděpodobností pokusit odpovědět na otázku: jak kolektivně překvapivé byly výsledky mistrovství světa 2022?
Narativní omyl
Je dobré si uvědomit, že pravděpodobnost, že ve všech 64 zápasech mistrovství světa nedojde k žádnému překvapení, je mizivá.
Existuje pouze 11 % šance, že favorit vždy vyhraje.
Na základě závěrečných kurzů Pinnaclu jsem vypočítal, že pravděpodobnost takové události je 6,5 x 10-17, tedy něco málo přes jedna ku trilionu. Pokud by se něco takového stalo, jednalo by se o jednu z nejúžasnějších událostí v historii lidstva. A přesto by mě zajímalo, kolik lidí kromě statistiků by tomu vůbec věnovalo pozornost, snad kromě poznámky, že je to extrémně nudné mistrovství světa.
Každý jiný scénář kombinací 64 výsledků má nižší pravděpodobnost. A potenciálních scénářů je hodně – 364 (pozn. redakce: každý ze 64 zápasů má tři možnosti výsledku – výhra domácích, remíza, výhra hostů), přesněji tedy 3 433 683 820 292 512 484 657 849 089 281.
V každém z nich dojde k překvapení (pokud budeme definovat překvapení jako neuskutečnění očekávaného výsledku neboli nevýhru favorita) a čím menší je pravděpodobnost 64možnostního scénáře, tím větší počet překvapení se v něm očekává.
Existuje pouze jediný způsob, jak k žádnému překvapení nedojde – musí nastat všechny předpokládané výsledky (pozn. redakce: všechny favorizované výsledky musí být naplněny). Naproti tomu existuje mnoho způsobů, jak může dojít k překvapení. Individuálně jsou jejich pravděpodobnosti pro každou kombinaci 64 zápasů menší, ale kolektivně jsou pravděpodobnější, než aby se žádné překvapení nestalo.
Uvažujme o jednoduchém binomickém příkladu 10 zápasů se dvěma možnými výsledky, kde má každý favorit 80% šanci na výhru a každý outsider 20% šanci. Existuje přibližně 11% šance, že všichni favorité vyhrají, ale 20% šance, že vyhrají 3 outsideři, a téměř 9% šance, že vyhrají čtyři outsideři.
Proč je pravděpodobnost, že tolik outsiderů vyhraje, tak vysoká? Individuálně jsou pravděpodobnosti pouze 0,17 % a 0,04 % (pro jedinou kombinaci výher tří respektive čtyř outsiderů), ale existuje mnoho možností, jak k nim může dojít – konkrétně 120 pro tři outsidery a 210 pro čtyři outsidery (pozn. redakce: znamená to, že máme 120 možných kombinací výher tří outsiderů a 210 možných kombinací výher čtyř outsiderů).
To vše představuje pouze jiný způsob, jak vám říct, že překvapení je potřeba očekávat. Přesto naše mozky často inklinují k tomu, že si z dat vytvářejí jednoduché, a někdy chybné příběhy, které dávají smysl pouze ve světě, jež považuje překvapení za méně pravděpodobná, než ve skutečnosti jsou.
Pokud by Japonsko neporazilo Španělsko a Německo, nepsali bychom o tom, ale statistika nám říká, že tyto překvapivé výsledky jsou v podstatě statistickou jistotou. Toto je jasný příklad narativního omylu.
Rozdělení pravděpodobnosti metodou Monte Carlo
Existuje pouze jediný způsob, jak vidět multiplikovanou sázku složenou ze 64 zápasů s pravděpodobností 6,5 x 10-17 (pozn. redakce: taková je pravděpodobnost toho, že v žádném zápase nedojde k překvapení, viz. výše). Nejméně pravděpodobná kombinace 64 zápasů, ve kterých zvítězí všichni outsideři, má pravděpodobnost 1,5 x 10-51 a existuje pouze jediný způsob, jak by k tomu mohlo dojít. Ale kolik způsobů bychom mohli vidět, např. při násobku pravděpodobnosti 10-25 nebo 10-30?
Vyřešit tyto výpočty algoritmicky je příliš složité. Abychom si vše dost usnadnili, je dobrým nápadem vytvořit simulaci Monte Carlo. Náhodným zamícháním výsledků zápasů podle definovaných pravděpodobností předpokládaných Pinnaclem můžeme vytvořit náhodně generovanou souborovou pravděpodobnost 64 zápasů.
Mnohonásobným zopakováním této simulace Monte Carlo spočítáme, kolikrát se vyskytla každá definovaná pravděpodobnost, například 10-25 nebo 10-30. Tímto způsobem můžeme definovat pravděpodobnostní distribuci, která nám umožní určit rozsah a pravděpodobnost možných výsledků 64 zápasů MS.
Práce s malými hodnotami pravděpodobnosti je však intuitivně poměrně obtížná. Můžeme nicméně aplikovat malou transformaci, která je učiní kognitivně zvládnutelnější: můžeme použít logaritmus. Například logaritmus (základ 10) pro 0.001 je -3; pro 0.000001 je to -6 a pro 0.000000000001 pak -12. Já budu pro své účely (základ e) používat přirozený logaritmus (ln) a vypustím záporné znaménko minus.
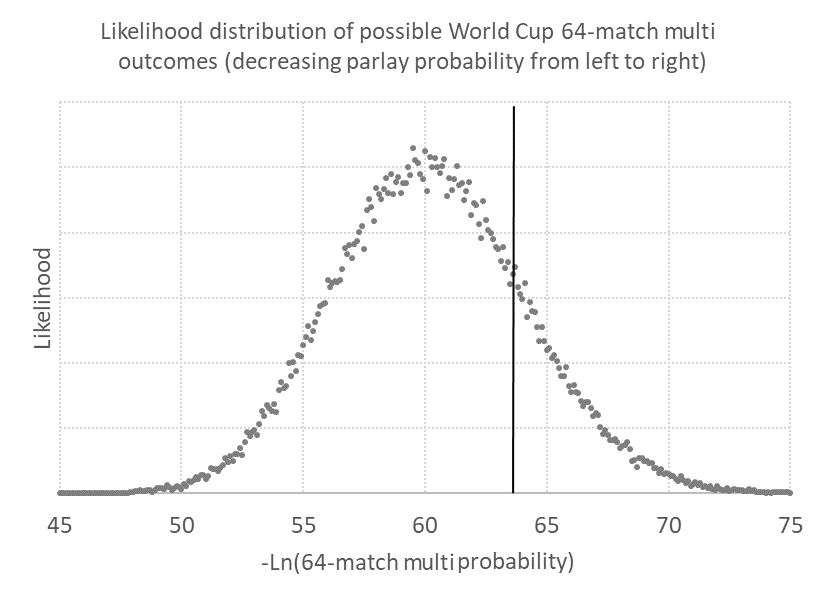
Moje Monte Carlo simulace obsahovala 100 000 cyklů pro 100 000 hodnot přirozeného logaritmu každé náhodně generované pravděpodobnosti kombinace výsledků 64 zápasů (s odstraněným záporným znaménkem). Tyto hodnoty jsem poté rozdělil do skupin a vytvořil následující graf pravděpodobnostní (či frekvenční) distribuce.
Zdroj: www.pinacle.com
Výsledky simulace jsou zobrazeny na grafu, kde osa x zahrnuje logaritmy pravděpodobností a osa y ukazuje četnost výskytu těchto hodnot. Celkový rozsah na ose x je od 37,3 (což představuje výhru všech 64 favoritů) do 117,1 (výhra všech 64 outsiderů), ale tyto pravděpodobnosti jsou nemožně malé.
Je tedy nutné zobrazit pouze nejpravděpodobnější výsledky, čímž získáme představu o tom, jaký je rozsah možností. Podíváme-li se na graf, vidíme, že je velmi pravděpodobné, že pro kombinace možností 64 zápasů bude hodnota na ose x někde mezi 45 a 75.
Tyto hodnoty odpovídají pravděpodobnostem zhruba 3 x 10-20 a 3 x 10-33. Pravděpodobnost výsledků kombinace 64 zápasů klesá, jak se po ose x pohybujeme doprava. Průměrná nebo nejpravděpodobnější pozorovaná kombinace výsledků je na ose x přibližně u hodnoty 60, což odpovídá kombinaci pravděpodobnosti 7.5 x 10-27.
V grafu je pomocí vertikální černé linie zanesena také lokace kombinace skutečných výsledků zápasů mistrovství světa. Hodnota na ose x je v tomto případě 63.5 (a pravděpodobnost kombinace výsledků je 2.7 x 10-28). To je přibližně 28krát méně než nejpravděpodobnější kombinace výsledků.
To sice vypadá jako ohromné číslo, ale graf vypovídá o něčem jiném. Můžete vidět, že tato linie není příliš daleko od středu (průměru) pravědpodobnostní distribuce. Ve skutečnosti bylo přibližně 20 % možných kombinací výsledků MS méně pravděpodobných než ty, které se nakonec skutečně staly.
Statisticky bychom to za překvapivé neoznačili. Pro to bychom potřebovali, aby se svislá čára posunula alespoň na hodnotu 70 na ose x, což by znamenalo, že jen méně než 1 % možných kombinací výsledků bylo méně pravděpodobných. To by odpovídalo pravděpodobnosti multiplikace přibližně 4 x 10-31, tedy téměř 700krát menší než té, ke které skutečně došlo. K tomu bychom museli vidět něco, jako že by Katar porazil Nizozemsko, Polsko porazilo Francii nebo Jižní Koreu, která by porazila Brazílii.
Bylo toto mistrovství světa překvapivé?
Na základě dat prezentovaných v tomto článku jsme se nyní dostali do fáze, kdy dokážeme odpovědět na mou původní otázku.
Ne, tolik překvapivé nebylo. Došlo sice k několika překvapením v jednotlivých zápasech, ale už víme, že ta můžeme na turnajích s tolika zápasy očekávat. Mnohem překvapivější by bylo, kdyby k žádnému překvapení nedošlo.
Filozoficky vzato, co překvapení opravdu znamená? To záleží především na našem očekávání výsledku zápasu. Představme si extrémní příklad, že by můj predikční model udělal z Walesu velké favority v zápasu s Anglií, z Ghany velké favority v zápase s Portugalskem, z Austrálie favority v zápase s Francií, z Kostariky favority proti Německu a tak dále ve všech zbylých 64 zápasech.
Nejspíše bych byl velmi překvapený, co že se to vlastně stalo. Je to kvůli tomu, že outsideři, které z nich můj model udělal, měli jednoduše štěstí, nebo byl můj predikční model špatný? V tomto případě je to samozřejmě nad slunce jasné, ale většinou je hranice mezi těmito dvěma možnostmi mnohem tenčí.
Odhady Pinnaclu na pravděpodobnost jednotlivých utkání ne vždy perfektně zachytily to, co se ve skutečnosti stalo. Je to kvůli smůle nebo jde o modelovou chybu?
Nyní už je mnohem obtížnější odpovědět. Můžeme ale říct, že protože neexistuje statisticky významný rozdíl mezi odhady Pinnaclu a skutečnými výsledky, máme dobré důvody pro to tvrdit, že model Pinnaclu není tak špatný.
Jinak řečeno, mistrovství světa (z pohledu Pinnaclu) nebylo z pohledu statistiky nijak zvlášť překvapivé. Výsledky byly méně pravděpodobné než u většiny jiných světových šampionátů (které měly statisticky o dva nebo tři překvapivé výsledky méně), ale ne nijak výrazně. Pokud by byl zaznamenán statisticky významný rozdíl, bylo by mnohem jednodušší názor Pinnaclu zpochybnit.
Můžeme tedy formulovat pravidlo: čím větší je rozdíl mezi očekáváním a realitou, tím větší je statistická pravděpodobnost, že náš model očekávání je chybný. Jak si predikční model Pinnaclu pro světový šampionát stál v porovnání s jinými sázkovými kancelářemi? To bude téma druhé části této série.
Další zajímavé články od stejného autora
EXKLUZIVNĚ: Úvod do teorie pravděpodobnosti a bayesovská inference v hazardu
01.09.2024 16:00 Přinášíme vám exkluzivní překlad odborného článku od sázkového analytika Bryana Nicholsona, který je mj. autorem několika knih o kurzovém sázení včetně jeho nejznámější publikace Hypnotised by Number. Bryanovou největší specializací je golf. Co je teorie pravděpodobnosti a jak funguje? Jak funguje Bayesova věta v praxi? Podmíněná pravděpodobnost v sázení na fotbal Bayesovská inference v hazardu Ti, kteří studovali teorii pravděpodobnosti…
Jak vydělat peníze na internetu prostřednictvím SportBreaku a SportBeetu
25.08.2024 10:40 Máte po práci nebo po škole volný čas navíc a rádi byste ho přetavili v peníze, ale na brigádu do call centra nebo Mekáče se vám nechce? Pak jste už pravděpodobně zkoušeli googlit fráze typu „Jak vydělat peníze na internetu“ nebo „Přivýdělek z domova“ apod., že? My jsme to také zkoušeli, takže víme, co jste našli. Jestli vás vyplňování dotazníků, založení vlastního webu, copywriting nebo natáčení videí neláká, máme pro vás nestandardní, ale…
EXKLUZIVNĚ: Goalimpact – Jak sázet díky objektivnímu hodnocení hráčů
10.08.2024 18:00 Přinášíme vám exkluzivní překlad odborného článek od Dr. Patricka Maye, který je v současné době zodpovědný startup Goalimpact. Ten objektivně hodnotí hráče pouze na základě měření jejich vlivu na konečný výsledek. Goalimpact spojuje jeho vědecké vzdělání s hlubokou láskou k fotbalu. Příběh společnosti Goalimpact Jak Goalimpact používá metriky a statistiku Případová studie z reálného života Jak může Goalimpact pomoci sázkařům? Původně…
TOP 10 servisů v červenci 2024
06.08.2024 20:15 Kterým servisům se v uplynulém měsíci nejvíce dařilo? Dozvíte se z našeho přehledu. Žebříček nejúspěšnějších servisů jsme seřadili podle celkového zisku. V červenci se dařilo! Ani jeden ze servisů se sice nepřehoupl přes magickou hranici 100 tisíc, ale desítka nejziskovějších servisů v červenci dohromady urvala 451 925 Kč, což je o více než sto tisíc více než v červnu. A to je na letní měsíc krásný výsledek, ze kterého máme radost nejen my,…
LOH 2024: Speciální balíčky od Dextera a Athletics Inside
25.07.2024 21:45 Sportovní událost roku je tu! Úvodní ceremoniál letních olmypijských her v Paříži je sice naplánován na pátek 26. července, ale už ve středu 24. byl odstartován fotbalový a rugbyový turnaj mužů. A s nimi přišly také první olympijské sázky našich verifikovaných servisů. My budeme tlačit především dva speciální olympijské balíčky, které si pro vás připravily dvě veleúspěšně poradenství, konkrétně ATHLETICS INSIDE a DEXTER. Pojďme si k nim říct pár…


