EXKLUZIVNĚ: Sázet velké objemy nebo vysokou hodnotu? To je, oč tu běží
29.12.2023 01:00
Přinášíme vám exkluzivní překlad odborného článku od sázkového analytika Josepha Buchdahla, který spravuje webové stránky www.football-data.co.uk, na kterém poskytuje historické výsledky, zápasové statistiky a údaje o kurzech. Je také autorem knih Fixed Odds Sports Betting: Statistical Forecasting & Risk Management (2003), How to Find a Black Cat in a Coal Cellar: The Truth about Sports Tipsters (2013) a Squares & Sharps, Suckers & Sharks: The Science, Psychology & Philosophy of Gambling (2016).
- Měli byste sázet vysoký objem sázek?
- Měli byste sázet na vysokou hodnotu?
- Porozumění očekávané hodnotě
Spolu s tématy jako je hodnota uzavíracích kurzů (pozn. redakce: kurzy těsně před začátkem události), rozlišení štěstí od dovedností a dobrá návratnost investice (ROI), se mezi začínajícími sázkaři objevuje ještě jedno téma: měl bych sázet vysoký počet sázek s nižší hodnotou nebo menší počet pečlivěji vybraných sázek s vysokou hodnotou?
Sázet velké objemy nebo vysokou hodnotu?
Tato otázka často rozděluje sázkaře na dva tábory. Jedni věří, že hodnota je nejdůležitějším aspektem sázky a jejich snahou bude vždy její maximalizace, přičemž odmítají příležitosti s nižší hodnotou, protože přinášejí menší zisk.
Druhá strana naopak trvá na tom, že je mnohem důležitější kontrolovat vliv variance nebo štěstí a nejlepším způsobem, jak to zvládnout, je sázet vysoký počet sázek, i když je jejich hodnota nižší. Kdo má pravdu? Právě to je tématem tohoto článku.
Stručně shrnuto, hodnota se v sázení používá k vyjádření očekávaného zisku sázkaře. Očekávaná hodnota sázky, neboli EV (z angl. expected value), nám ukazuje, kolik můžeme očekávat, že na na jedné sázce (v průměru) vyhrajeme nebo prohrajeme.
Nejjednodušším způsobem, jak ji vypočítat, je vydělit kurzy sázkové kanceláře skutečným kurzem a odečíst 1. To je ekvivalentní s tím, že skutečnou pravděpodobnost výsledku sázky vydělíme implikovanou pravděpodobností, kterou nám předkládá sázková kancelář a odečteme 1. Nejsložitějším úkolem při sázení je vědět, jak zjistit skutečnou pravděpodobnost výsledku. Tím se ale v tomto článku zabývat nebudeme.
Předpokládejme, že skutečný kurz nějaké příležitosti je 2.00. Pokud sázková kancelář omylem nabídne kurz 2.10, očekávaná hodnota bude 2.10 / 2.00 - 1 = 0,05 čili 5 %. Po 1 000 sázkách za 1 jednotku se stejnou očekávanou hodnotou by měl v průměru sázkař získat 50 jednotek. Pokud by sázková kancelář nabídla kurz 2.25, očekávaná hodnota by byla 12,5 %. Obvykle je to ale sázkař, kdo udělá chybu. Pokud by přijal kurz 1.95, očekávaná hodnota takové sázky by byla -2,5 %.
Samozřejmě, že průměr v tomto případě znamená nejpravděpodobnější výsledek, ale štěstí nebo smůla mohou při sérii sázek vést k rozdílným výsledkům. Očekávaný profit z 1 000 sázek s kurzem 2.00 při 5% hodnotě může být 50 jednotek, ale pokud máme smůlu, získáme méně, a naopak, pokud máme štěstí, můžeme získat více.
V jiném článku o rozložení možných výsledků jsem se zabýval rozsahem možných výnosů (YIELD) ze sázek. Níže přikládám graf rozložení možných výnosů, které můžeme od tohoto scénáře očekávat.
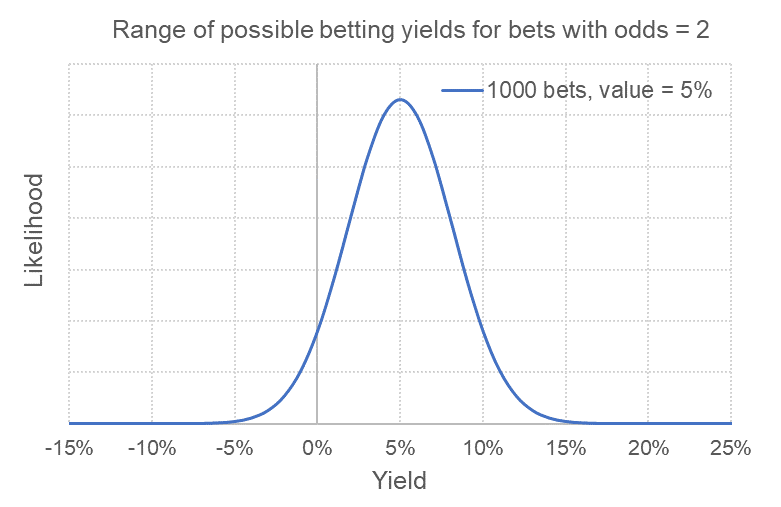
Pro ty, které zajímá matematika této distribuce, je na následujícím odkazu jednoduchá Excel kalkulačka, která vysvětluje základní metodiku, zatímco v knize Monte Carlo or Bust – Simple Simulations for Aspiring Sport Bettors najdete mnoho dalších podrobností.
Z rozložení je patrné, že nejpravděpodobnějším výsledkem, za předpokladu, že očekávaná hodnota 5 % je správná, je YIELD 5 %. Z 1 000 sázek o hodnotě 1 jednotky bychom tak získali profit 50 jednotek.
Můžeme také pozorovat rozsah možností od extrémní smůly po velké štěstí. Je velmi nepravděpodobné, že bychom skončili s YIELDEM menším než -5 % nebo větším než 15 %. Zároveň můžeme posoudit pravděpodobnost ztráty – jedná se o oblast pod vlnovou křivkou nalevo od svislé osy při 0% zisku. Ta se dá vypočítat a činí okolo 6 %.
Podívejte se, co se s distribucí možných výsledků stane, když změníme počet sázek. Níže jsem provedl stejný výpočet pro 100 sázek a rozložení porovnal s prvním grafem. Zvětšil jsem měřítko osy x, aby se obě křivky do grafu vizuálně vešly, nicméně modrá křivka je zcela stejná jako předtím. Důležité je zde srovnání.
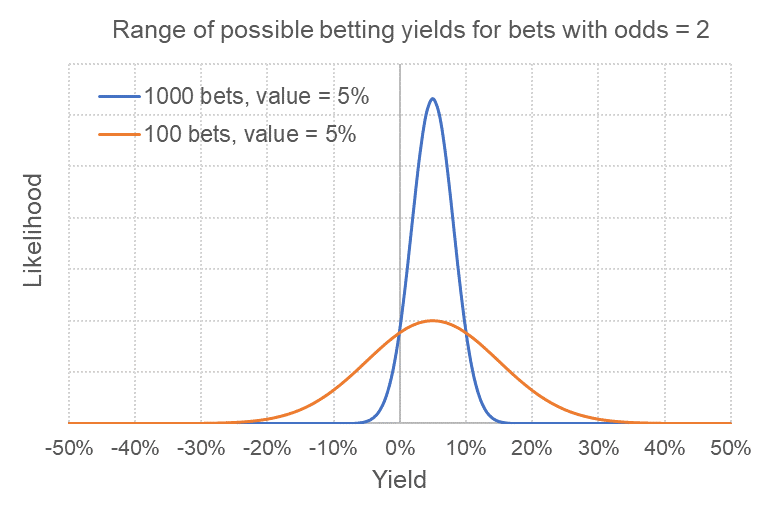
Vyčnívají dvě věci. Zaprvé, existuje mnohem širší rozsah možností s relativně větší pravděpodobností vyšších ztrát i vyšších profitů, ale relativně menší pravděpodobností dosažení nejočekávanějšího výsledku. Statisticky řečeno, se zvětšila odchylka. Jinými slovy, štěstí hraje větší roli.
Zadruhé, tím pádem se zvětšila oblast pod vlnovou křivkou v oblasti záporného výnosu na zhruba 31 %. To znamená, že bez ohledu na 5% hodnotu, kterou na těchto 100 sázkách máme, existuje zhruba třetinová šance, že budeme ve ztrátě. Více sázek sníží rozptyl možných výsledků tím, že sníží vliv štěstí a pravděpodobnost ztráty v případě, že držíme kladnou očekávanou hodnotu sázky.
1:0 pro všechny, kteří obhajují vyšší objem sázek.
Ale moment, sázkaři, kteří jsou vybíravější, tak činí právě proto, že se zaměřují na sázky s vyšší hodnotou. To znamená, že jejich očekávaný výnos bude vyšší. Proto musíme uvedenou oranžovou křivku upravit tak, aby tuto skutečnost odrážela.
Předpokládejme, že sázkař sázející kurzy s vysokou hodnotou má při 100 sázkách průměrnou očekávanou hodnotu 20 %. Jak bude jeho křivka vypadat v porovnání se sázkařem sázejícím vyšší objemy? Pojďme se na to podívat.
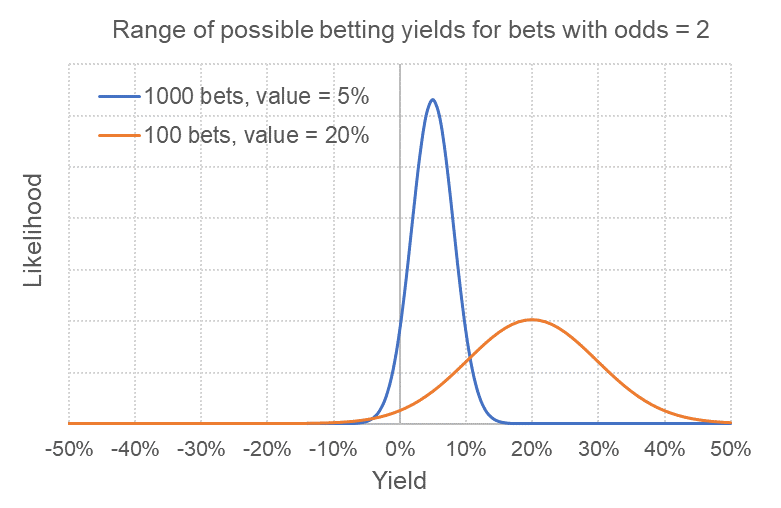
Rozptyl výnosů sázejícího s vysokou hodnotou má stále stejný tvar, ale posunul se o 15 procentních bodů doprava a očekávaný (průměrný) YIELD nyní činí 20 %. Rozptyl výsledků je stále stejně široký, ale je zde daleko méně ztrátových výsledků. Ve skutečnosti jsou to pouze 2 %, což je mnohem méně než u vysokoobjemového sázkaře s 1 000 sázkami a 5% očekávanou hodnotou.
Vhodným způsobem pro porovnání rozptylu těchto dvou sázkařů je metrika známá jako z-skóre. Při ní se očekávaný výnos dělí směrodatnou odchylkou rozptylu. V podstatě jde o míru očekávaného výnosu na jednotku rozptylu, a čím je toto číslo vyšší, tím lépe. Ve finančnictví se tato metrika nazývá Sharpův poměrový koeficient. Směrodatná odchylka σ je mírou rozptylu rozdělení. Její druhá mocnina je jednoduše rozptyl.
Pro sérii sázek se stejnými kurzy, o, ji lze vypočítat pomocí následující rovnice:
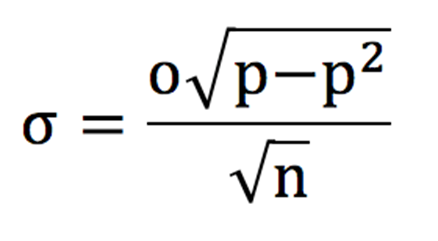
p je skutečná pravděpodobnost výhry sázky a n je počet sázek. Tuto rovnici lze spolehlivě použít i v situacích, kdy mají sázky rozdílné kurzy, ale velikosti vkladů jsou stejné. V tomto případě o představuje jednoduše průměrné kurzy.
Abychom vypočítali p, jednoduše přičteme 1 k očekávanému YIELDU (získáme očekávanou návratnost) a vydělíme tuto hodnotu kurzem. Pro našeho sázkaře s vysokým objemem sázek s očekávaným výnosem 5 % (či 0,05), platí: p = (1+0,05)/2 = 0,525 neboli 52,5 %, a tedy σ = 0,0316 (či 3,16%).
Přibližně dvě třetiny všech možných výnosů v distribuci sázkaře s vysokým objemem budou 3,16 % nad nebo pod očekávanou hodnotou 5 %. Nyní můžeme vypočítat z-skóre: 5 % / 3,16 % = 1,58.
Provedeme-li stejný výpočet pro sázkaře s vysokou hodnotu, dostaneme z-skóre 2,04, což je vyšší hodnota než u vysokoobjemového sázkaře.
Skóre souboje mezi objemem a hodnotou je nyní 1:1.
Větší objem snižuje rozptyl výsledků, ale selektivnější přístup a dosažení vyššího očekávaného výnosu, může zlepšit vaše z-skóre a očekávaný výnos na jednotku variance.
Zatím jsem si pouze libovolně vybíral očekávané hodnoty a počet sázek. Náš sázkař s vysokou hodnotou měl čtyřikrát vyšší očekávanou hodnotu než sázkař s vysokým objemem sázek, a to při pouhé desetině sázek, ale jak reálná tato čísla jsou?
Sázky s 20% hodnotou je při kurzech 2.00 velmi složité najít. Můžeme počítat s tím, že jich budeme schopni na každých 1 000 sázek s očekávanou hodnotou 5 % najít 100? Musíme najít způsob, jak to zjistit.
Proxy metoda hodnocení míry hodnoty na sázkovém trhu spočívá ve studiu pohybů kurzů. Předpokládáme-li, že uzavírací kurzy v průměru férově reflektují skutečnou pravděpodobnost – což je téma, kterému jsem se věnoval dříve – lze velikost předchozích pohybů použít k výpočtu hrubé míry předchozí očekávané hodnoty, která mohla v kurzech být.
Čím větší je pohyb, tím vyšší je očekávaná hodnota. To neznamená, že uzavírací kurzy nikdy nemají hodnotu, ale spíše, že v průměru je rozdíl mezi dvěma sadami kurzů rozumným odrazem skutečné dostupné hodnoty.
Na základě rozsáhlého souboru počátečních a uzavíracích kurzů na fotbalové zápasy u Pinnaclu jsem vypočítal relativní dostupnost očekávané hodnoty, která by reálně mohla být dostupná. To je znázorněno níže.
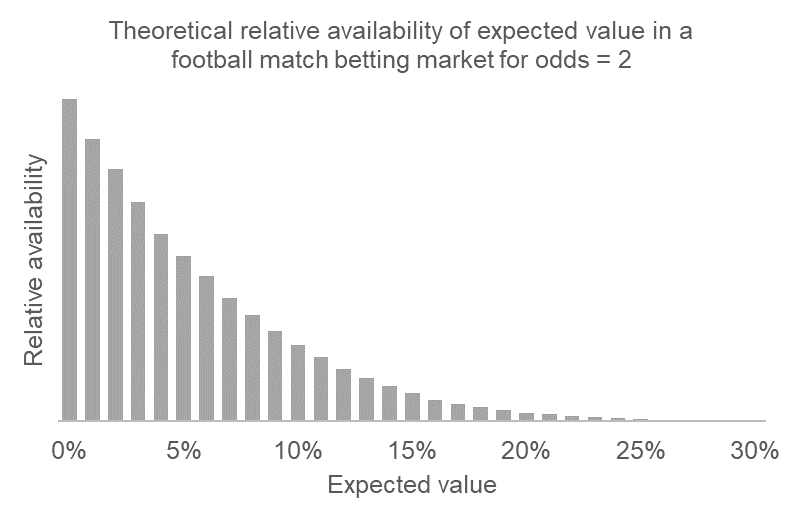
Na tomto trhu bylo asi dvacetkrát více dostupných sázkových příležitostí, kde byla očekávaná hodnota alespoň 5 %, než těch, kde byla alespoň 20 %. To znamená, že pokud by byl náš vysokoobjemový sázkař schopný najít 1 000 příležitostí s očekávanou hodnotou 5 %, sázkař vysoké hodnoty by na stejném trhu ve stejném časovém horizontu reálně nebyl schopen najít více než 50 příležitostí, což je zhruba polovina toho, s čím jsem původně počítal. Vezmeme-li v úvahu tuto informaci, přepočítejme nyní z-skóre pro sázkaře s vysokou hodnotou s touto menší velikostí vzorku.
Nyní je 1,44, což je nižší hodnota než hodnota u sázkaře sázejícího vysoké objemy. Pravděpodobnost ztráty po těchto 50 sázkách je 7,5 %. S ohledem na relativní dostupnost různé výše očekávané hodnoty z tohoto scénáře vyplývá, že sázkař sázející vysoké objemy sázek zvolil z hlediska řízení rizika lepší strategii.
Objem se ujímá vedení 2:1 nad hodnotou.
Dosud jsem se zabýval pouze výnosy (YIELDEM), ale ve skutečnosti každého sázkaře nakonec více zajímá skutečný profit. 5% YIELD z 1 000 sázek vynese sázkaři ze sázek v hodnotě 1 jednotky zisk 50 jednotek. Naproti tomu 20% YIELD z 50 sázek poskytne sázkaři profit pouze 10 jednotek.
Objem navyšuje své vedení nad hodnotou na 3:1.
Samozřejmě, každý zastánce Kellyho kritéria bude poukazovat na to, že sázky s vyšší očekávanou hodnotou by měly znamenat vyšší vklady. V tomto případě bychom pro stejné kurzy se čtyřnásobnou hodnotou mohli obhájit čtyřnásobnou hodnotu vkladu. Tím tedy zvyšujeme očekávaný profit na 40 jednotek, což je mnohem blíže k 50 jednotkám prvního sázkaře.
Hodnota snižuje na rozdíl jednoho gólu díky kontroverzní penaltě.
Konečné skóre v duelu mezi objemem a hodnotou končí těsným vítězstvím 3:2 pro objem. Ačkoli byl tento příklad spíše zábavou, pomáhá ilustrovat konkurenční vlivy snižování variance (zvýšením počtu sázek) a zvyšování očekávané hodnoty (díky větší selektivitě tipů).
Zdá se, že minimálně na fotbalových trzích neexistuje dostatečná nabídka příležitostí s vyšší očekávanou hodnotou, která by ospravedlnila strategii větší selektivity ve srovnání se strategií, která se snaží maximalizovat objem a snižovat varianci. Nicméně výsledek je velmi těsný; různé trhy mohou poskytovat různé příležitosti, které by mohly jazýčky na miskách vah převážit na druhou stranu.
Snižování variance je pro sázkaře vždy trefa do černého, ale tento myšlenkový experiment by nám měl pomoci pochopit, že se nejedná o jediný faktor, který musíme brát v potaz.
Sázkaři s vyššími objemy se budou nadále pošklebovat sázkařům pátrajícím po vysoké hodnotě a naopak. Ve skutečnosti ale pomůže lepší pochopení relativního vlivu objemu a hodnoty každému ambicióznímu sázkaři maximalizovat šanci na dosažení požadovaných výsledků.
Zdroj: Obrázky použity z původního článku dostupného na webu pinnacle.com.
Další zajímavé články od stejného autora
Betano – registrační bonus 500 Kč a další doplňkové bonusy
29.07.2024 12:00 Společnost Betano přišla na český trh teprve v roce 2022. Už tehdy však byla v zahraničí oceněná coby jedna z nejlepších sázkových kanceláří a rychle si tak našla své klienty i u nás. Vděčí tomu nejen pestré kurzové nabídce, ale rozhodně i zajímavým bonusům které na hráče čekají. Pojďte se s námi podívat, co si pro nové klienty Betano připravilo. Betano nabízí 500 Kč do hry za registraci Registrační bonusy jsou mezi hráči nesmírně oblíbené a…
EXKLUZIVNĚ: Data stojící za udělováním karet ve fotbale: Co vzít v úvahu před sezónou 2023/2024
22.07.2024 21:30 Přinášíme vám exkluzivní překlad odborného článek od Andrewa Beasleyho, jehož profesní kariéra se sice posunula od studia médií k práci v bance, ale jeho skutečnou vášní byl vždy fotbal. Poté, co pozoroval, jak se v jeho milovaném sportu rozšířila data, rychle se tomuto trendu přizpůsobil a nyní se věnuje analýze fotbalových statistik. Jakou roli hraje v rozhodování VAR? Využití statistik společnosti Opta k analýze udělování karet Diskuse,…
Kingsbet | Nová sázková kancelář
22.07.2024 10:00 Na našem trhu se nachází celá řada známých sázkovek, mezi kterými nechybí jména jako Tipsport, Betano či Fortuna. V roce 2024 však na trh vstoupilo další zajímavá sázková kancelář Kingsbet, která má rozhodně také co nabídnou. Pojďte se společně s námi podívat, co všechno vám nabízí. O Kingsbet Možná už vás hra na klasických sázkových kancelářích nudí a chcete si vyzkoušet nějakou tu novinku. Pak pro vás může být Kingsbet zcela ideálním…
Fortuna | Věrnostní body
15.07.2024 12:00 Mnoho českých sázkových kanceláří nabízí pro své pravidelné hráče zajímavou formu odměn prostřednictvím věrnostních bodů. Výjimkou není ani velmi oblíbená Fortuna, který tento systém na své platformě rovněž nabízí. Pojďte se společně s námi dozvědět, jak věrnostní body Fortuny fungují. Co jsou to věrnostní body na Fortuně? Věrnostní body od Fortuny jsou způsob, prostřednictvím kterého Fortuna odměňuje sázející, jež hrají prostřednictvím její…
Fortuna – registrační bonus 300 Kč
11.07.2024 12:00 Sázková kancelář Fortuna je nejstarší sázkovou kanceláří na českém trhu. Působí na něm už od roku 1991 a od té doby si stačila vybudovat velmi silnou hráčskou základnu. Ta se neustále rozrůstá nejen díky široké kurzové nabídce, ale také početným bonusům. Nejzajímavější pro hráče je jistě bonus za registraci, který na Fortuně činí rovných 300 Kč. Pojďte se s námi o něm dozvědět více. Bonus 300 Kč za registraci u Fortuny Registrační bonusy…


